Math - dérivée : correction exercice 2 du Niveau débutant

a) Calcul de la dérivée y ' de la parabole

y ' = (x² + 1) ' = 2x

b) Calculer graphiquement la pente de la tangente à la parabole en x = -2

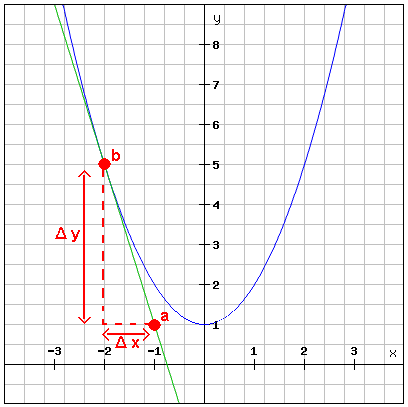
Pente de la tangente =

c) Trouver l'équation de cette tangente

L'équation d'une droite est y = ax + b, où le coefficient a est la pente de la droite.

Or la pente de notre tangente vaut –4.

Par conséquent l'équation de cette tangente sera
y = -4x + b.

Mais que vaut le terme indépendant b ?

Sachant que notre tangente est tangente à la parabole en x = -2, donc en y = (-2)² + 1 = 5, nous pouvons à présent calculer le terme indépendant b de la droite de pente a = -4 passant par le point (-2 ; 5) :

        Equation de la tangente : y = -4x + b,

        nous savont que (x ; y) = (-2 ; 5) vérifie cette équation.

        Donc 5 = -4(-2) + b,

        d'où 5 + 4(-2) = b,

        finalement b = 5 - 8 = -3.

        Conclusion : l'équation de la tangente est y = - 4x - 3

d) Calculer la dérivée de cette tangente

y ' = (-4x - 3) ' = - 4

e) Tirer une conclusion sur les réponses trouvées en b) et en d)

La dérivée de l'équation de la tangente, calculée en d), est égale à la pente de cette tangente, calculée en b).

Calculer une dérivée revient à calculer une pente et inversément

.

Il est également intéressant de noter que la dérivée de la parabole a pour équation f '(x) = (x² + 1) ' = 2x.

f '(x) = 2x est l'équation de la dérivée de la parabole mais c'est aussi l'équation des pentes des tangentes à cette parabole en différents points de la courbe.

Ou encore, f '(x) = 2x exprime la pente de la courbe pour différentes valeurs de x.

Par exemple, que vaut la pente de la parabole en x = -2 ?

f '(-2) = 2(-2) = -4.

Ou encore que vaut la pente de la courbe en x = 1 ?

f '(1) = 2(1) = 2

.