Exercice de mathématique corrigé et résolu en détail gratuitement : comment dériver une fonction de x, f(x) - Apprendre à dériver une fonction en math.
Dérivée : correction exercice 1 du Niveau intermédiaire
Soit la fontion y = 3x2 + 2 et la fonction y = (1/2)x3 - 1, on demande :
a) Calculer la dérivée y ' de ces deux fonctions
-
y ' = (3x2 + 2) ' = 6x
y ' = (0,5x3 - 1) ' = 1,5x2 = (3/2)x2
b) Calculer, pour ces deux courbes, la pente de leur tangente en x = 1
à l'aide de leur dérivée
La pente de la tangente à une courbe en x = 1 est la valeur de sa dérivée en x = 1.
y ' = f '(x) = 6x
f '(1) = 6 . 1 = 6 = pente de la tangente à la courbe y = 3x2 + 2 en x = 1-
y ' = f '(x) = (3/2)x2
f '(1) = (3/2) . 12 = 3/2 = pente de la tangente à la courbe y = (1/2)x3 - 1
en x = 1
c) de trouver l'équation de ces 2 tangentes
-
Pour y = 3x2 + 2, sa tangente en x = 1 est tangente à la courbe en le point de coordonnée x = 1 et y = 3 . 12 + 2 = 5, je sais donc que ma tangente passe par le point (1 , 5). Je sais aussi que la tangente a une pente de 6 et donc son coefficient angulaire vaut a = 6. Calculons à présent l'équation de cette tangente :
Equation générale d'une droite : y = ax + b
Equation de ma tangente : y = 6x + b ...
... passant par le point (1 , 5) : 5 = 6 . 1 + b
d'où 5 - 6 = b
Donc b = -1Conclusion : la tangente à y = 3x2 + 2 en x = 1 est y = 6x - 1
-
Même raisonnement pour la tangente à la courbe y = (1/2)x3 - 1 en x = 1
La tangente passe par le point de coordonnée x = 1
et y = 0,5 . 13 - 1 = -0,5 = -1/2
Equation de ma tangente de pente a = 3/2 par le point (1 , -1/2) :
y = (3/2)x + b
-1/2 = (3/2) . 1 + b
donc -(1/2) - (3/2) = b
d'où b = -4/2 = -2
Conclusion : la tangente à y = (1/2)x3 - 1 en x = 1 est y = (3/2)x - 2
d) Représenter les courbes et leur tangente sur un graphique
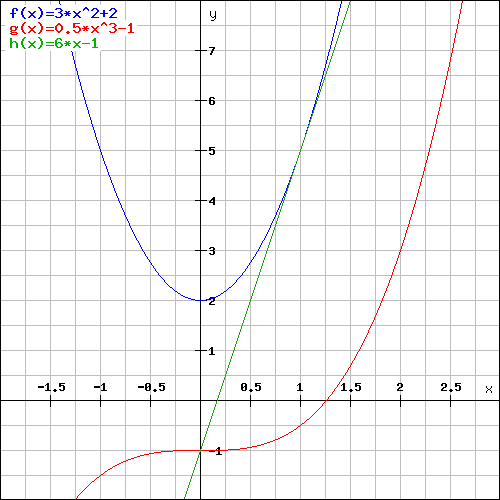
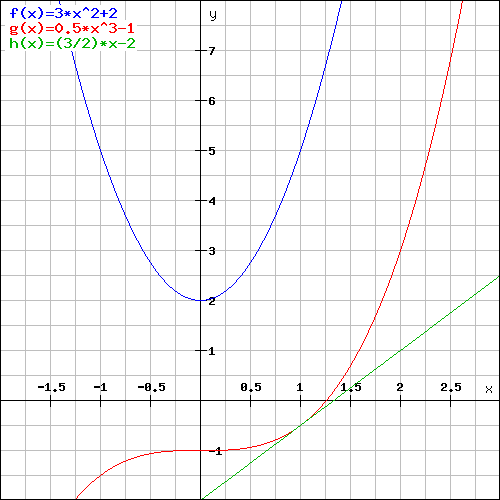
Ces deux graphiques ont été tracé à l'aide de notre outil graphique Le Grapheur.