Accueil > Dérivée > Exemples de dérivées > Exercices résolus > Niveau intermédiaire > Correction exercice 2



Comment dériver une fonction trigonométrique ? Vous allez apprendre ci-dessous à calculer la dérivée d'un sinus, d'un cosinus et d'une tangente.

Dérivée : correction exercice 2 du Niveau intermédiaire


Soit la fonction fonction trigonométrique dérivée - sinus dérivée, cosinus dérivée, dériver tangente - exercice correction gratuite, on demande :


a) Calculer la dérivée f '(x) de cette fonction


exercice math trigonométrie dérivée : comment dériver un sinus, un cosinus, une tangente.


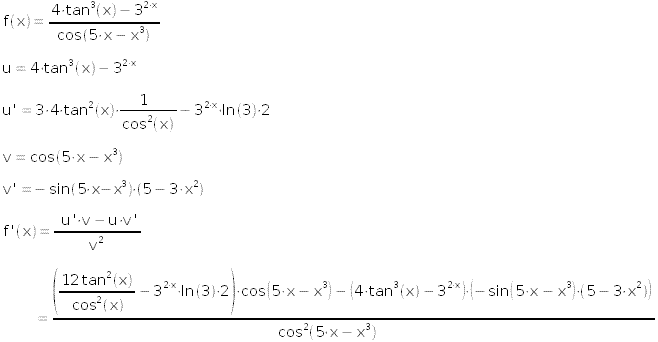
b) Déterminer l'équation cartésienne de la tangente à f(x) en x = 0


Equation générale d'une droite : y = ax + b où a = f '(0)

dérivée cos, dériver sin, dérivée tan - trigonométrie maths exercices dérivées

f '(0) = -2 ln(3) est le coefficient angulaire a de la tangente à la courbe en x = 0.
Soit l'équation de cette tangente : y = -2 ln(3) x + b, je sais qu'elle passe par le
point x = 0 et y = f(0) = (4 tan3(0) - 30) / cos(0) = -1 / 1 = -1
Donc l'équation de cette tangente par le point (0 , -1) est :

      y =-2 ln(3) x + b

      -1 = -2 ln(3) 0 + b

      d'où b = -1

      Conclusion: la tangente à pour équation y = -2 ln(3) x - 1

Voici le graphique de votre courbe et de sa tangente, tracées grâce au Grapheur (décochez la case "Erreur" afin d'éviter l'affichage du message d'erreur intempestif).

cos dérivée, sin derivee, tg dériver, apprendre à dériver sinus, cosinus et tangente en trigonometrie



← Dérivées : exercices niveau intermédiaire