Notions de math abordées: première bissectrice, équation d'une courbe, tangentes parallèles, équation générale d'une droite, dérivée, équation de la tangente.
Dérivée : correction exercice 4 du Niveau intermédiaire
Soit l'équation d'une courbe f(x) = 2x3 - 6x + 5, déterminez
les points de la courbe où les tangentes sont parallèles à la première
bissectrice. Vous devez également trouver l'équation de ces tangentes et
représenter la courbe et les tangentes graphiquement.
f(x) = 2x3 - 6x + 5
f '(x) = 6x2 - 6
La première bissectrice est la droite y = x qui coupe le plan x-y en deux angles de 45 degrés.
La pente de cette droite vaut 1. Par conséquent, toute autre droite parallèle à la première bissectrice aura, dans son équation y = ax + b, un coefficient a valant 1.
Nous savons donc que nos tangentes auront pour équation y = 1x + b. Mais que vaut b ?
Nous recherchons le point (x1 , y1) de la courbe f(x) = 2x3 - 6x + 5 où la tangente a une pente
de 1. Donc f '(x1) = 1, c'est-à-dire que la dérivée de la courbe en x = x1 doit valoir un. Nous allons calculer x1:
Il existe donc seulement deux points sur la courbe où la tangente à la courbe est parallèle à la première bissectrice. Et ces deux points
sont:
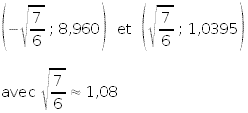
|
L'équation générale de ces tangentes est y = 1x + b |
|
|
y = x + b 8,96 = -1,08 + b b = 10,04 La tangente à la courbe f(x) |
y = x + b 1,0395 = 1,08 + b b = - 0,04 La tangente à la courbe f(x) |
Le graphique suivant représente la fonction f(x) et ses deux tangentes parallèles à la première bissectrice :
Comment tracer le graphique de mes équations ? A l'aide du Grapheur !