Résolution exercice de math gratuit en ligne : corrigé exercice de dérivée mathématique gratuitement online. Apprendre à dériver une fonction avec des exercices résolus sur internet.

Dérivée : correction exercice 1.1 du Niveau avancé

1. Optimisation: 1.1 Deux nombres se cachent

Deux nombres se cachent, cependant nous savons que leur somme vaut 12. Trouver ces deux nombres:

a) Si la somme de leur carré est minimale

Si la somme de leur carré x² et y² est minimale nous devons avoir simultanément:

(x² + y²)' = 0 et (x² + y²)' ' > 0

En effet, nous nous souvenons que:

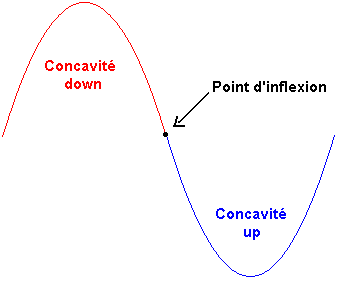
La valeur de x qui annule la dérivée première d'une fonction nous donne la coordonnée x d'un extremum (peu importe qu'il soit minimum ou maximum). Lorsque la dérivée seconde d'une fonction est positive, nous pouvons dire que nous avons une concavité up, c'est-à-dire que la courbe nous sourit. Donc un minimum implique une dérivée seconde positive. Tandis que lorsque la dérivée seconde est négative, la courbe présente une concavité down, c'est-à-dire un sourire inversé (ou un visage fâché). Donc un maximum implique une dérivée seconde négative.

Récapitulatif de nos trois équations:

(1) x + y = 12

(2) (x² + y²)' = 0

(3) (x² + y²)' ' > 0

Ces trois conditions doivent être réunies simultanément (c'est à dire en même temps: (1) ET (2) ET (3) doivent être vrais tous les trois).

Remplaçons (1') y = 12 - x dans les deux autres équations et nous obtenons:

(2') (x² + (12 - x)²)' = 0

(3') (x² + (12 - x)²)' ' > 0

Dérivons (2'):

(x² + (12 - x)²)' = 0

2x + 2(12-x)(-1) = 0

2x -24 + 2x = 0

24 = 4x

x = 24/4 = 6

Or on sait grâce à (1) que x + y = 12 d'où:

y = 12 - x = 12 - 6 = 6

Vérifions que le point (x , y) = (6 , 6) vérifie l'équation (3') (x² + (12 - x)²)' ' > 0:

(x² + (12 - x)²)' ' > 0

(2x + 2(12-x)(-1))' > 0

2 + 2 > 0

4 > 0

Or 4 est bien plus grand que zéro, nous confirmons donc que la dérivée seconde de
(x² + y²) est positive et que nous avons donc affaire à une fonction concave up. (6 , 6) sont donc bien les coordonnées d'un minimum.

Conclusion : 6 et 6 sont les deux nombres dont la somme fait 12 et dont la somme de leur carré est minimale.

Nous vous proposons de tracer l'équation x² + (12-x)² à l'aide du Grapheur sur un interval compris entre -10 et 10 pour x, et entre -10 et 80 pour y.
Tracez également sa dérivée à l'aide du bouton Dérivée du Grapheur. Vous constaterez alors que le minimum de la fonction à lieu pour une valeur de x = 6, et que la dérivée première est bien nulle en cette valeur de x.

b) Si le produit de l'un et du carré de l'autre est maximal

(1) x + y = 12

(2) (x² . y)' = 0

(3) (x² . y)' ' < 0

En effet, la dérivée seconde, dans l'équation (3), doit être négative afin d'avoir une courbe concave down et ainsi un extremum qui sera maximum cette fois-ci.

(1') y = 12 - x

(2') (x² . (12 - x))' = 0

(3') (x² . (12 - x))' ' < 0

Nous allons trouver la valeur de x grâce à (2'):

(x² . (12 - x))' = 0

2x . (12 - x) - x² = 0

24x - 3x² = 0

3x( -x + 8) = 0

d'où x = 0 ou x = 8

Vérifions si les deux valeurs de x trouvées vérifient l'équation (3'):

(x² . (12 - x))' ' < 0

(24x - 3x²) ' < 0

(24 - 6x) < 0

24 < 6x

24/6 < x

4 < x

d'où x > 4, donc la valeur x = 8 est correcte tandis que x = 0 est à rejeter car elle ne satisfait pas l' équation (3'). Graphiquement cela signifie qu'en x = 0 la fonction n'est pas concave down mais bien concave up, x = 0 correspond à la coordonnée d'un extremum minimum or nous recherchons un maximum. C'est pourquoi nous rejetons cette valeur.

Conclusion: x = 8 et y = 12 - x = 12 - 8 = 4. Nos deux nombres sont donc 8 et 4.

c) Si le produit de l'un et du cube de l'autre est maximal

(1) x + y = 12

(2) (x³ . y)' = 0

(3) (x³ . y)' ' < 0

(1') y = 12 - x

(2') (x³ . (12 - x))' = 0

(3') (x³ . (12 - x))' ' < 0

Trouvons x à l'aide de l'équation (2'):

(x³ . (12 - x))' = 0

3x² . (12 - x) - x³ = 0

36x² - 4x³ = 0

4x²(9 - x) = 0

d'où x = 0 ou x = 9

Les valeurs de x = 0 et x = 9 vérifient-elles l'équation (3') ?

(x³ . (12 - x))' ' < 0

(36x² - 4x³)' < 0

72x - 12x² < 0

12 . x . (-x + 6) < 0

Si x = 0, alors la dérivée seconde 12 . x . (-x + 6) est égale à 0 or elle devrait être inférieure à 0. Par conséquent x = 0 est une valeur à rejeter parce qu'elle ne satisfait pas l'équation (3'). Graphiquement, x = 0 correspond à un point d'inflexion, c'est-à-dire à un point de la courbe où la concavité est entrain de changer, il y a une transition d'une concavité up vers une concavité down ou inversément. Un point d'inflexion est un point de la courbe ou la concavité n'est ni down ni up, mais transitoire. Or nous recherchons un maximum et non un point d"inflexion. Il faut donc rejeter la valeur de x = 0.

Tandis que si x = 9, alors la dérivée seconde 12 . x . (-x + 6) est égale à -81 ce qui est bien inférieur à zéro et satisfait donc notre équation (3').

Conclusion: si x = 9 alors y = 12 - x = 12 - 9 = 3. Nos deux nombres sont donc 9 et 3.