Avant d'aborder les exercices de maths du niveau avancé, soyez certains de maîtriser le niveau débutant et le niveau intermédiaire.

A qui s'adresse ce cours de maths avancé ?

• à ceux qui veulent vraiment comprendre l'utilité d'une dérivée de fonction par le biais d'exercices de dérivée mathématique plus pratiques appliqués à la biologie, la médecine, l'économie, l'actualité,...

• aux étudiants qui souhaitent entreprendre des études scientifiques et ainsi se mettre (ou se remettre) à niveau en math,

• aux élèves qui désirent préparer un examen de math ou un concours d'entrée scientifique pour une école d'ingénieur ou une école de commerce par exemple,

• aux étudiants qui sont en première année d'étude à l'université, en classe préparatoire ou en haute école.

Sommaire

1. Optimisation

• 
  1.1 Deux nombres se cachent

• 1.2 Le plus gros container

• 1.3 Un fermier désire clôturer son champ

• 1.4 Récolter son riz à temps pour maximiser ses bénéfices

• 1.5 Chaine de montage de Henry Ford

2. Dérivées bêtes et méchantes

• 
  2.1 Dériver et simplifier

• 2.2 Dériver et simplifier

• 2.3 Dériver et simplifier

• 2.4 Dériver et simplifier

3. Dérivée et graphe

• 
  3.1 Dérivée et calcul de pente

• 3.2 Durée du jour à Fairbanks, en Alaska

4. Dérivée appliquée à la biologie, à la médecine et à l'économie

• 
  4.1 Déclin d'une population de bactéries

• 4.2 Dériver graphiquement

• 4.3 Démographie chez les drosophiles

• 4.4 Population arctique de phoques et d'ours

• 4.5 Le diamètre de votre trachée se réduit 33% lors d'une toux

• 4.6 Coût et revenu en économie: maximisez votre bénéfice

1. Optimisation

1.1 Deux nombres se cachent
Solution 1.1

Deux nombres se cachent, cependant nous savons que leur somme vaut 12. Trouver ces deux nombres:

a) si la somme de leur carré est minimale,

b) si le produit de l'un et du carré de l'autre est maximal,

c) si le produit de l'un et du cube de l'autre est maximal

1.2 Le plus gros container
Solution 1.2

Le prix de l'acier ayant presque doublé en moins d'un an en passant de 400 euros la tonne en 2007 à 700 euros la tonne en 2008, il est capital d'économiser la matière. Il s'agit donc de construire des containers aussi grands que possible tout en utilisant une surface d'acier la plus faible possible en produisant le moins de déchets métalliques. C'est pourquoi on vous demande de trouver les dimensions du plus gros container (sans couvercle) que l'on peut fabriquer à partir d'une feuille d'acier rectangulaire de 24 m² en découpant des carrés égaux des quatre coins de la feuille et en redressant les côtés. L'un des côtés de cette feuille d'acier doit mesurer 6 m pour des raisons de facilité de production.

1.3 Un fermier désire clôturer son champ
Solution 1.3

Un fermier souhaite entourer un champ rectangulaire et le diviser en deux parties égales à l'aide d'une clôture parallèle à l'un des côtés du champ. Il fait donc appel à vous, grand spécialiste en optimisation de clôture. Il vous demande de trouver les dimensions du champ d'aire maximale (superficie max) que l'on peut entourer et diviser avec 1200 m de clôture seulement.

1.4 Récolter son riz à temps pour maximiser ses bénéfices
Solution 1.4

Comme vous le savez, le prix du riz à l'exportation a doublé depuis février 2007 pour atteindre un sommet historique en février 2008 avec un prix de plus de 40 eurocents/kg. Le tout causant des problèmes de nutrition dans les régions du monde les moins riches. Si un fermier effectue sa récolte de riz aujourd'hui, il obtiendra 1200 kg valant 40 eurocents le kg. Pour chaque semaine d'attente, la récolte augmente de 100 kg mais le prix baisse de 2 eurocents par kg. Quand devrait-il effectuer sa récolte pour maximiser ses bénéfices (profit maximum)?

1.5 Chaine de montage de Henry Ford
Solution 1.5

Dans une usine de construction de voitures, les pièces sont assemblées grâce au génie de l'Américain Henry Ford (grand sympathisant nazi et antisémite notoire, soit dit en passant, qui inventa et mit au point la chaîne de montage en 1906). Cependant, avant d'être assemblées, les portières de la voiture doivent être peintes. C'est pourquoi une énorme cuve cylindrique en acier, d'un volume de 64 m³, stocke de la peinture. Nous vous demandons de trouver les dimensions de la cuve pour que la quantité de métal nécessaire à sa construction soit minimale. Et cela dans un souci d'économiser la matière et donc les ressources limitées de la terre en général. Remarque importante: la cuve est totalement fermée.

2. Dérivées bêtes et méchantes

Dérivez les fonctions suivantes et simplifiez au maximum votre résultat.

2.1    
          Solution 2.1

2.2    
   
     Solution 2.2

2.3    
   
     Solution 2.3

2.4    
   
     Solution 2.4

3. Dérivée et graphe

3.1 Dérivée et calcul de pente         Solution 3.1

Soit le graphe suivant :

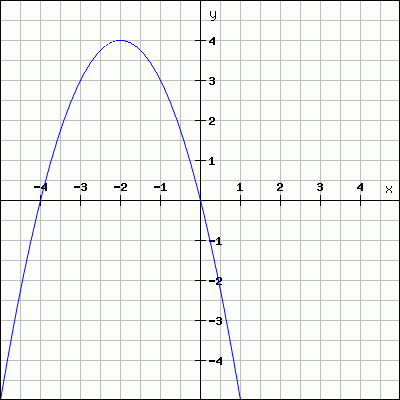
On vous demande:

a) D'estimer la pente de la courbe en x = -2 et en x = -4 par le calcul du , donc par le calcul de la pente de la tangente à la courbe.

b) Dans mon infinie bonté, je vous annonce à présent que l'équation de cette parabole est y = -(x + 2)² + 4, calculez alors la valeur de sa dérivée en x = -2 et en x = -4.

c) Tirez une conclusion des réponses trouvées en a) et en b).

Remarque: pour résoudre cet exercice vous devrez imprimer ce graphique. Si vous n'avez pas d'imprimante, décalquez la parabole et les axes avec un crayon et une feuille de papier blanche que vous déposerez sur votre écran.

3.2 Durée du jour à Fairbanks, en Alaska        Solution 3.2

Le graphique suivant montre le nombre d'heures de clarté sur une journée à Fairbanks en Alska, et ce pour chaque jour de l'année entre le 1er janvier et le 31 décembre.

Ainsi, par exemple, le 1er septembre il n'y a que 5 heures de clarté à Fairbanks. Et le 1er janvier la durée du jour est inférieure à 1 heure. Répondez aux questions suivantes en estimant la pente sur le graphique en heures/jour. Faites l'hypothèse que chaque mois de l'année ne comporte que 30 jours afin de simplifier le problème.

a) A quelle date le nombre d'heures de clarté quotidienne augmente-t-il le plus d'un jour à l'autre ? Et quel est ce taux d'augmentation (en heures/jour).

b) Que vaut la dérivée de la courbe à la date trouvée en a).

c) Voyez-vous des jours de l'année où le nombre d'heures de clarté quotidienne ne varie pas d'un jour à l'autre ? Si oui, pouvez-vous nous dire quels sont ces jours ? Et que vaut la dérivée de la courbe ces jours-là ?

d) A quelles dates le taux de variation du nombre d'heures de clarté quotidienne est
positif ? Est négatif ? En déduire le signe de la dérivée en ces dates ?

Remarque: pour résoudre cet exercice vous devrez imprimer ce graphique. Si vous n'avez pas d'imprimante, décalquez la courbe et les axes avec un crayon et une feuille de papier blanche que vous déposerez sur votre écran.

4. Dérivée appliquée à la biologie, à la médecine et à l'économie

4.1 Déclin d'une population de bactéries        Solution 4.1

Lorsqu'un bactéricide a été introduit dans un milieu nutritif où une population de bactéries croissait, la population a continué à croître pendant un certains temps mais peu après elle s'est arrêtée de croître et a commencé à décliner. La taille de la population à l'instant t est f(t) = 10⁶ + 10⁴ . t - 10³ . t².
f(t) représente le nombre de bactéries et t représente le temps en heures. On vous demande de trouver le taux de croissance, , au temps t = 0 sec,
t = 5 heures et t = 10 heures.

4.2 Dériver graphiquement        Solution 4.2

Dessinez, précisément, la dérivée du graphique suivant

Remarque: pour résoudre cet exercice vous devrez imprimer ce graphique. Si vous n'avez pas d'imprimante, décalquez la courbe et les axes avec un crayon et une feuille de papier blanc que vous déposerez sur votre écran.

4.3 Démographie chez les drosophiles        Solution 4.3

Les populations qui se développent dans un environnement clos commencent toujours par grossir lentement parce que au début il y a très peu d'individus pour procréer. Ensuite, à mesure que le nombre d'individus en âge de se reproduire augmente, la population croît plus rapidement. Mais très vite, les ressources se font plus rares, l'espace et la nourriture ne sont plus aussi abondants qu'aux premiers jours, la croissance de la population ralentit. On a atteint la capacité portante de l'environnement. Cette situation est décrite par une fonction mathématique dont le graphe (ci-dessous) représente l'évolution de la taille d'une population de drosophiles (mouches) au cours du temps:

On vous demande:

a) Utilisez une technique graphique pour tracer la fonction dérivée de cette courbe. Quelles unités utiliserez-vous pour l'axe horizontal et vertical du graphe de la fonction dérivée ?

b) Quels sont les jours durant lesquels la population semble grossir / grandir le plus vite ? Le plus lentement ?

Remarque: pour résoudre cet exercice vous devrez imprimer ce graphique. Si vous n'avez pas d'imprimante, décalquez la courbe et les axes avec un crayon et une feuille de papier blanc que vous déposerez sur votre écran.

4.4 Population arctique de phoques et d'ours        Solution 4.4

Le graphique suivant montre le nombre de phoques et d'ours dans une population arctique. L'évolution de ces deux populations a été étudiée sur une période de 600 jours:

Nombre initial de phoques = 3000.

Nombre initial d'ours = 400

Remarquez que le nombre de phoques augmente au début alors qu'ils se reproduisent beaucoup. Cependant, les ours mangent les phoques et, la nourriture étant abondante, eux aussi se reproduisent. A mesure que le nombre d'ours augmente, la croissance de la population de phoques ralentit, pour finalement amener au déclin. Le graphique suivant montre la dérivée de la population de phoques en fonction du temps (il s'agit donc de la dérivée de la courbe bleue claire du graphe ci-dessus).

Vous devez à présent répondre aux questions suivantes:

a) Quelles est la valeur de la dérivée de la population de phoques en fonction du temps lorsque le nombre de phoques est le plus important ? Lorsqu'il est le moins important ? Expliquez ce que signifie le résultat obtenu.

b) Quelle est la taille de la population de phoques lorsque sa dérivée est la plus grande ? Lorsque sa dérivée est la plus faible. Expliquez également la signification du résultat obtenu.

c) En quelles unités doivent être exprimées la pente du premier graphique et l'axe vertical du second graphique ?

4.5 Le diamètre de votre trachée se réduit 33% lors d'une toux        Solution 4.5

Lorsque vous toussez, votre trachée se contracte pour augmenter la vitesse avec laquelle l'air est expulsé vers l'extérieur (voir Bernouilli). Ceci nous amène à nous poser la question suivante: de combien de centimètres le rayon de votre trachée doit-il se réduire pour contracter cette dernière et maximiser ainsi la vitesse d'expulsion de l'air. La formule suivante décrit une relation entre v (vitesse d'expulsion de l'air au sein de votre trachée lorsque vous toussez) et r (rayon de la trachée).

v = c . (r₀ - r) . r²

v en cm/s,

c est une constante positive dont la valeur dépend de la longueur de votre trachée,

r₀ est le rayon de votre trachée au repos,

r est le rayon de votre trachée lorsque vous toussez.

On vous demande :

a) De démontrer que l'air est expulsé avec une vitesse v maximum lorsque r = (2/3).r₀ , c'est-à-dire lorsque le rayon de la trachée s'est réduit de 33,33%. Le fait le plus remarquable, c'est que les images prisent aux rayons X confirment cette valeur de 33,33% de contraction de la trachée.

b) De tracer le graphe de v(r) et de sa dérivée v'(r) à l'aide du Grapheur. Prenez r₀ = 2 cm et c = 1. Remplacez la lette r par la lettre x dans votre équation. Vérifiez ensuite, graphiquement, que le rayon r correspondant à la vitesse d'expulsion maximum correspond bien aux deux tiers de la valeur r₀. Vérifiez également graphiquement la valeur de la dérivée à cet endroit (elle doit être nulle).

4.6 Coût et revenu en économie: maximisez votre bénéfice        Solution 4.6

Il existe en économie, des relations mathématiques entre le revenu, r(x), et le bénéfice, b(x). Le revenu est l'argent reçu lorsque l'on a produit (et donc vendu) x articles. Quant au bénéfice, on le calcule en soustrayant les coûts, c(x), au revenu.

r(x) = revenu engendré par la production (et donc la vente) de x articles. c(x) = coûts engendrés par la production de x articles (main d'oeuvre à payer, chauffage des bâtiments, loyer des bureaux et hangars,...) b(x) = r(x) – c(x) = bénéfice dû à la production (et donc à la vente) de x articles.

Vous avez remarqué que le revenu, le coût et le bénéfice sont toutes des fonctions du nombre d'articles produits, x. Aussi, la dérivée du revenu par rapport à x, r'(x), nous donne le revenu marginal. Or nous savons qu'une dérivée n'est autre que le calcul d'une pente, par conséquent le revenu marginal r'(x) représente un (pour un interval sur r et sur x infiniment petit), ce qui nous donne la pente de la courbe à différents niveaux de production, c'est à dire pour différentes valeurs de x. Nous savons ainsi, grâce au revenu marginal, quel sera le revenu supplémentaire engendré, , pour produire un article de plus, . Il en va de même pour la dérivée du coût par rapport à x, c'(x), qui nous donne le coût marginal et donc le coût supplémentaire lié à la production d'un article de plus, et ce pour différents niveaux de production.

r'(x) = revenu marginal. c'(x) = coût marginal.

Le graphique ci-dessous met en évidence le fait important suivant:

Le bénéfice maximum et positif (= gain) survient à un niveau de production (donc à une valeur de x spécifique) pour lequel le revenu marginal est égal au coût marginal: b(x) = max si r'(x) = c'(x) et b(x) > 0

En effet, dans notre exemple, l'entreprise travaille avec un bénéfice positif à droite du point d'égalité. Et ce parce que la courbe du revenu est au-dessus de celle du coût donc b(x) = r(x) – c(x) > 0. L'entreprise gagne alors de l'argent. Le bénéfice maximum et positif (= gain) survient, quant à lui, toujours à droite du point d'égalité (dans notre exemple dumoins), lorsque les deux tangentes vertes sont parallèles, c'est à dire lorsque b'(x) = c'(x) – r'(x) = 0 (nous obtenons la coordonnée x des extrema en égalant la dérivée première du bénéfice à zéro) donc lorsque c'(x) = r'(x).

Cependant, remarquez qu'a l'extrême droite du graphique les coût sont supérieurs aux revenus, l'entreprise travaille à perte. Cela peut arriver sutie à une inefficacité des opérations dûe à un trop haut taux de production combiné à un marché saturé sur lequel on ne parvient plus à vendre la marchandise.

A gauche du point d'égalité, l'entreprise opère également à perte. Les coûts sont supérieurs aux revenus, on ne produit pas assez de marchandise et la vente ne parvient pas à couvrir les coûts de production. L'entreprise se trouve dans une situation où
b'(x) = 0; c'(x) = r'(x) mais b(x) est min et < 0. Il s'agit d'un bénéfice minimum et négatif, donc d'une perte maximum !

La perte maximum survient elle aussi pour une valeur de x où les tangentes vertes sont parallèles, mais on la distingue du bénéfice maximum car la courbe du coût est au-dessus de celle du revenu: c(x) > r(x) donc b(x) < 0 donc perte.

On vous demande :

Etant donné les équations suivantes

r(x) = 10 . x

c(x) = x³ - 6.x² + 15.x + 5

x = nombre d'articles produits, en milliers d'unités.

a) Y a-til un niveau de production qui maximise le bénéfice ? Si oui, lequel.

b) Trouvez un niveau de production qui minimise le coût moyen de production.

c) Le niveau de production qui maximise le bénéfice et celui qui minimise le coût moyen son-il différents ? Fort différents ? Ou égaux ?

d) Après avoir répondu aux questions a), b), c) et réalisé tous vos calculs, utilisez
Le Grapheur pour tracer r(x), c(x) et leur dérivée respective afin de vérifier vos réponses et de visualiser graphiquement ce qui se cache derrière ces fonctions et dérivées « mystiques ».