Accueil > Dérivée > Exemples de dérivées > Exercices résolus > Niveau avancé > Correction exercice 3.1



Math, Dérivée et graphe : la dérivée f'(x) est une fonction mathématique qui donne la pente de la tangente à la courbe f(x) en un point x de votre choi. Calculer graphiquement la pente en un point d'une courbe est une manière d'estimer graphiquement la valeur de la dérivée de la fonction en ce point.

Dérivée : correction exercice 3.1 du Niveau avancé


3. Dérivée et graphe: 3.1 Dérivée et calcul de pente


Remarque: pour résoudre cet exercice vous devrez imprimer ce graphique. Si vous n'avez pas d'imprimante, décalquez la parabole et les axes avec un crayon et une feuille de papier blanche que vous déposerez sur votre écran.

Soit le graphe suivant :

Le sommet d'une parabole a toujours une pente nulle et donc une tangente horizontale. Et donc une dérivée qui vaut zéro en ce point de la parabole.

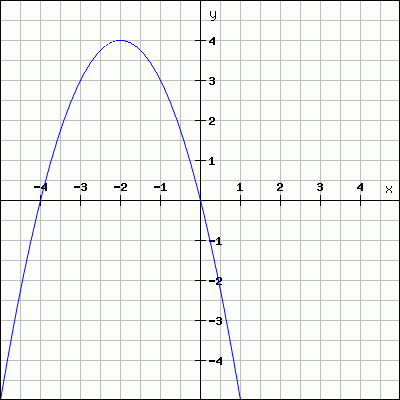
On vous demande:

a) D'estimer la pente de la courbe en x = -2 et en x = -4 par le calcul du Dérivée et graphe : le calcul de la pente de la tangente à la parabole permet d'estimer graphiquement la valeur de la dérivée d'une fonction en un point de la courbe., donc par le calcul de la pente de la tangente à la courbe.


Voici la parabole avec ces deux tangentes (que vous avez tracées à la latte sur le graphique imprimé) en x = -4 et en x = -2

La dérivée f'(x) est une fonction qui calcule la pente des tangentes à la courbe f(x) en un point x de votre choi.

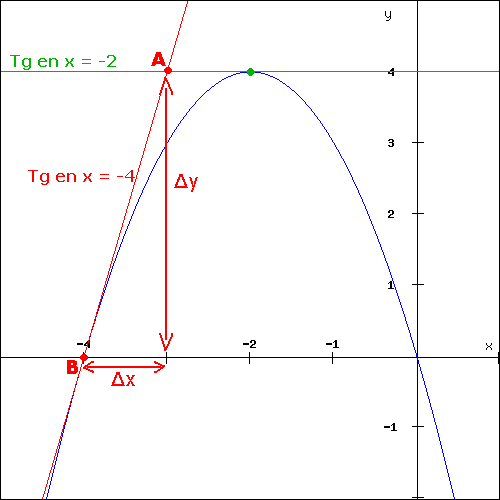
La pente de la courbe en x = -2 s'obtient en calculant la pente de la tangente à la courbe en x = -2:
Parabole, tangente, dérivée et calcul de pente = 0 / Equation de parabole, tangente et valeur de la´derivée = 0. Cette pente est nulle car la tangente à la courbe en ce point est parfaitement horizontale. Retenez que le sommet d'une courbe a toujours une pente nulle et donc une tangente horizontale.

Nous trouvons la pente de la courbe en x = -4 en traçant, à la latte, la tangente à la parabole en ce point. Nous calculons ensuite sa pente comme suite:
L'équation d'une parabole et dérivée d'une parabole. = (yA - yB) / (xA - xB) = (4 - 0) / ( -3 - (-4) ) = 4. La parabole a donc une pente de 4 en x = -4.


b) Dans mon infinie bonté, je vous annonce à présent que l'équation de cette parabole est y = -(x + 2)2 + 4, calculez alors la valeur de sa dérivée en x = -2 et en x = -4.


Soit y = f(x) = -(x + 2)2 + 4
Alors f '(x) = -2.(x + 2) = -2x - 4 .

f '(-2) = -2.(-2) - 4 = 0.
f '(-4) = -2.(-4) - 4 = 4.


c) Tirez une conclusion des réponses trouvées en a) et en b).


La dérivée de la fontion en x = -2 est f '(-2) = 0. Cela correspond exactement à la valeur de la pente de la courbe calculée en x = -2 et qui valait elle aussi 0.

La dérivée de la fonction en x = -4 est f '(-4) = 4 et cela correspond également à la valeur de la pente de la parabole en x = -4.

Conclusion: La fonction dérivée f '(x) est une équation qui vous donne la pente de la courbe f(x) en un point x de votre choi.



← Dérivées : exercices niveau avancé