Math et dérivée appliqué à la biologie : calcul de dérivée et croissance d'une population de bactéries - Utiliser la dérivée de la fonction f(t) pour calculer le taux de croissance d'une population de bactéries en fonction du temps t - Prévoir l'évolution du nombre de bactéries au temps t grâce aux dérivées de fonctions.
Dérivée : correction exercice 4.1 du Niveau avancé
4. Dérivée appliquée à la biologie, à la médecine et à l'économie: 4.1 Déclin d'une population de bactéries
Lorsqu'un bactéricide a été introduit dans un milieu nutritif où une population de bactéries croissait, la population a continué à croître pendant un certains temps mais peu après elle s'est arrêtée de croître et a commencé à décliner. La taille de la population à l'instant t est f(t) = 106 + 104 . t - 103 . t2.
f(t) représente le nombre de bactéries et t représente le temps en heures.
On vous demande de trouver le taux de croissance, , au temps t = 0 sec,
t = 5 heures et t = 10 heures.
Pour saisir pleinement la subtilité de cet exercice, il est important de visualiser le graphe de la fonction f(t) = 106 + 104 . t - 103 . t2 :
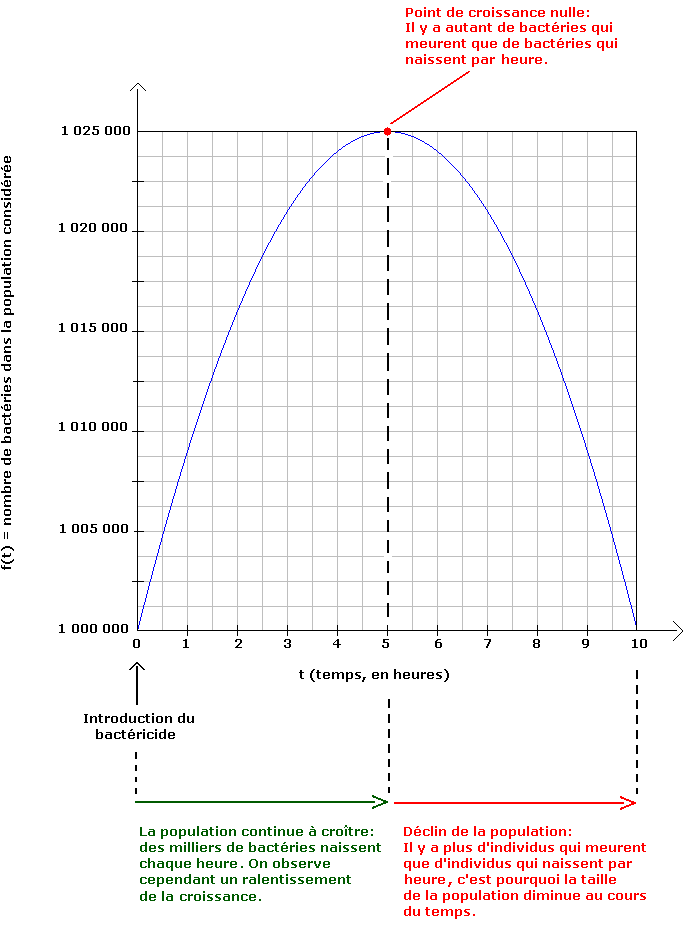
Comment répondre aux questions posées ?
A l'aide de la dérivée de la fonction : f '(t). Vous pouvez également vérifier vos réponses en traçant la tangente à la courbe en t = 0, t = 5 et t = 10 et en calculant ensuite la pente de chacune des tangentes. Si vous tracez chaque tangente précisément, les réponses que vous trouverez avec le calcul de la dérivée devraient être très proches des réponses trouvées graphiquement par le tracé de la tangente.
Réponses :
En t = 0 heures : taux de croissance = + 10.000 individus/heure. Cela signifie qu'à l'instant initial, au moment où l'on insère le bactéricide au sein de la population de bactéries, il y a 10.000 nouveaux individus qui "apparaissent" par heure. Pour être tout à fait précis, il faut dire que le nombre de naissances moins le nombre de morts par heure donne un taux net de + 10.000 bactéries/heure.
En t = 5 heures : taux de croissance = + 0 individus/heure. Cela signifie que 5 heures après avoir introduit le bactéricide dans la culture de bactérie, la population de microorganismes entre dans une phase temporaire de stagnation où le nombre de morts/heure est exactement égal au nombre de naissances/heure. Le taux de croissance devient donc nul.
En t = 10 heures : taux de croissance = - 10.000 individus/heure. Cela signifie que le nombre de morts est supérieur au nombre de naissances. Ainsi, le nombre de naissances moins le nombre de morts par heure donne une perte nette de 10.000 individus par heure. Une dérivée négative (-10.000) correspond ici à un taux de croissance négatif donc à une décroissance : le déclin de la population de bactéries est entrain de s'opérer.
Vous ne vous en sortez pas avec le calcul de la dérivée, le tracer des tangentes et le calcul de leur pente ? Ne vous inquiétez pas, des mathématiciens chevronnés sont en ligne pour vous venir en aide. Demandez-leur un coup de pouce sur les deux forums de mathématiques suivants :